多くの人にとって最もなじみのある統計量といえば「平均」ではないでしょうか。
ただ、「平均」というと一般的には足して2で割る形式の相加平均(算術平均、単純平均とも言います)が使われることが多いでしょうが、「平均」の求め方にもいくつかあり、相加平均を用いてはいけないケースもあります。
「平均」の平均は全体の平均?
部品メーカーのX社では、3つの工場で同じ製品を生産しています。
ある週における不良品率が
A工場: 3%
B工場: 2%
C工場: 7%
だった場合、会社全体の不良品率は
(3+2+7)/3=4%
という計算で正しいでしょうか。
もし、3工場の生産数が同じであれば問題ないのですが、生産数が異なる場合には3工場それぞれの不良品率からだけでは全体の平均を出すことはできません。
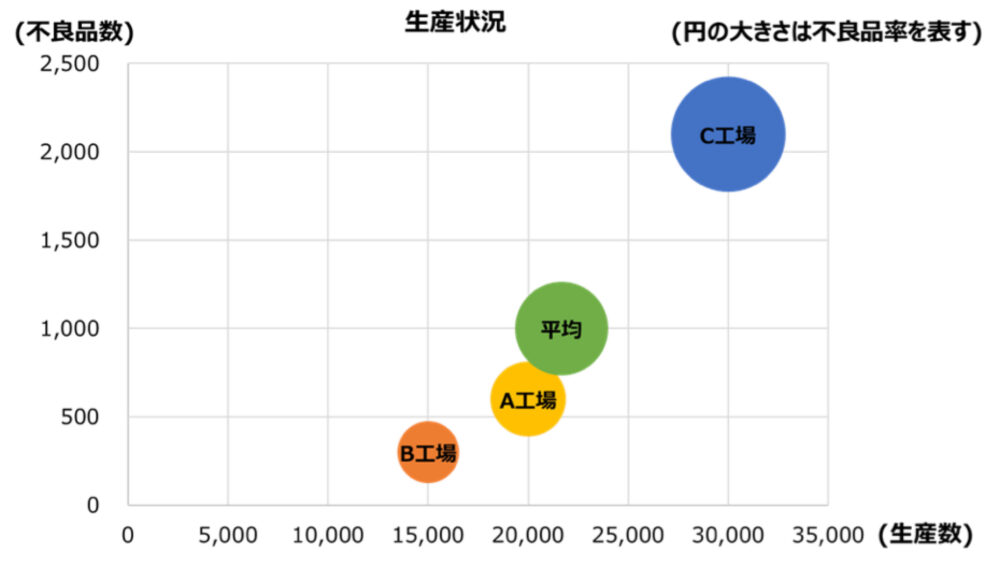
実際の3工場における生産状況は以下の通りでした。
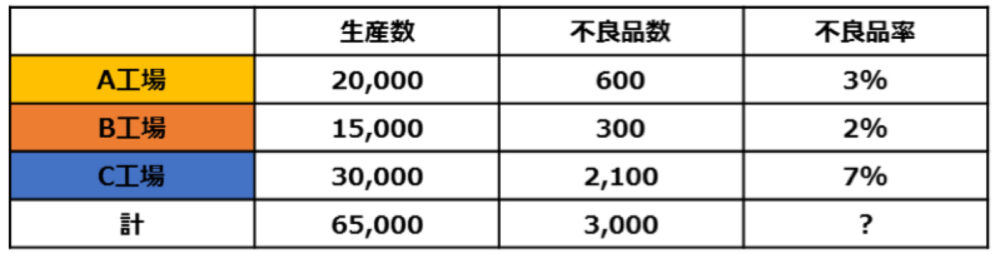
この場合、全体の不良品率は、3,000&➗65,000≒4.6%となります。
変化率の平均を求めるには?
では、今度はX社の売上高の変化について考えてみましょう。
X社は業績好調で年々売上を伸ばしており、過去3年間におけるX社の売上高の増加率(対前年比)は
一昨年: 30%増
昨年: 20%増
今年: 70%増
でした。
この時、3年間の平均増加率はどうやって求めればよいのでしょうか。
相加平均だと
(30+20+70)/3=40%
となるわけですが、売上高の変化以外にも、例えばGDP成長率や物価変動、投資の運用利回りといった変化率の平均を出す場合には、相加平均ではなく相乗平均を用いなければなりません。
相乗平均(幾何平均とも言います)は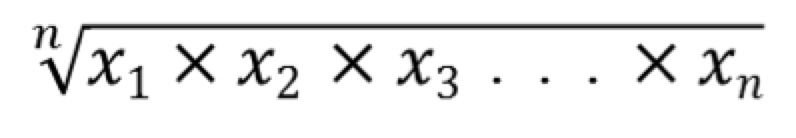
で求められ、上記の例だと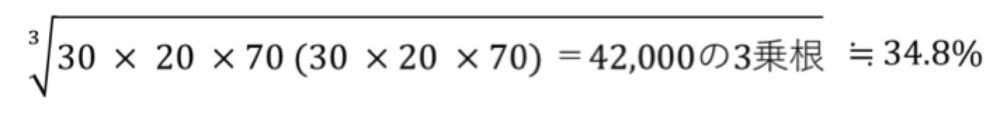
となります。
一般的に相加平均の値は相乗平均よりも大きくなりますので、相乗平均を使うべきところを相加平均で計算すると数値を多めに見誤ってしまうことになります。
「平均」は身近な統計量で、ふだんよく目にする、あるいは自分で計算する機会も多いかと思いますが、それだけに適切に使われているかどうか留意したいものです。
(参考)
Excelで累乗(根)を計算するには「^(ハット)」を用います。
例えば、42,000の3乗根は「=42000^(1/3)」と入力すれば求められます。
【次はこちらもおすすめ】





