先日行われた大学入学共通テストは、昨年に比べ全体的に問題が難しくなったとされ、特に数学Ⅰ・Aの平均点は昨年に比べ20点以上も下がったようです(100点満点)。
数学Ⅰ・Aには統計に関する問題が含まれます。
一部、用語の意味や公式を知らないと解けない問題もありますし、文章量が多いため、制限時間がある実際の受験時は結構大変だったかと思います。
ただ、基本的にはコツコツ時間をかければ、しばらく数学から離れてしまっている人でも解ける問題です。
統計の勉強がてらチャレンジしてみましょう。
今年の統計に関する問題は、難しくはないが解くのに時間がかかる
では早速、今年の数学Ⅰ・Aの統計に関する問題をみていきます。
と言っても、著作権の問題があるため、ここで試験問題を掲載するわけにはいきません。
共通テストの問題は、新聞各社などのサイトに掲載されていますので、「共通テスト 2022 問題」で検索して、[数学Ⅰ・A]-[第2問]-[2]の問題(PDFだと12ページからになります)をご覧ください。
問(1)
(1)は、ヒストグラム(度数分布図)を正しく読み取れるかどうかの問題です。
問題に取り組む前に用語の確認をしておきましょう。
| 中央値 | データを小さい(大きい)順に並べた時にちょうど真ん中にくる値 |
| 第1四分位数/第3四分位数(しぶんいすう) | 中央値より小さいデータの並びの真ん中の値が第1四分位数、中央値より大きいデータの並びの真ん中の値が第3四分位数。中央値は第2四分位数でもある。 |
| 四分位範囲 | 第1四分位数と第3四分位数の差分 |
| 階級 | ヒストグラムでは、横軸で示される一定間隔のデータ区分 |
| 階級値 | それぞれの階級における真ん中の値 |
29か国のデータが問題になってますので、中央値は「15番目」の値、第1四分位数は「7番目と8番目の間(平均)」の値、第3四分位数は「22番目と23番目の間(平均)」の値となります。また、階級の幅は15人刻みになっています。
図1(2009年)と図2(2018年)を見て、階級ごとの国数を地道に数えていくと
2009年度と2018年度の中央値が含まれる階級は、ともに「30~44人(階級値は37)」。
従って、「ケ」の答えは②[両者は等しい]
2009年度と2018年度の第1四分位数が含まれる階級は、ともに「15~29人(階級値は22)」。
従って、「コ」の答えも②[両者は等しい]
2009年度の第3四分位数が含まれる階級は「60~74人(階級値は67)」、2018年度の第3四分位数の方は「45~59人(階級値は52)」。
従って、「サ」の答えは⓪「2018年のほうが小さい」
2009年度は「0~14人」はないものの「165~179人」が1か国あるのに対し、2018年度の最大値は「120~134人」まで。
従って、範囲を聞いている「シ」の答えは⓪「2018年のほうが小さい」
このヒストグラムからだけでは第1四分位数、中央値、第3四分位数の値そのものはわからず、四分位範囲も求められない。
従って、四分位範囲を比較する「ス」の答えは③「これら二つのヒストグラムからだけでは両者の大小を判断できない」
データの範囲などは図を見比べてすぐに分かるでしょうが、四分位数がどの階級に含まれるかは直感的には分かりづらいのでコツコツ数えていく必要がありそうです。
問(2)
続いて(2)は、箱ひげ図とヒストグラムの数字を読み取って、両者を組み合わせた散布図の形状はどれかを答えさせる問題です。
まず、箱ひげ図の見方をおさらいしておきます。
問題にある図3の場合は
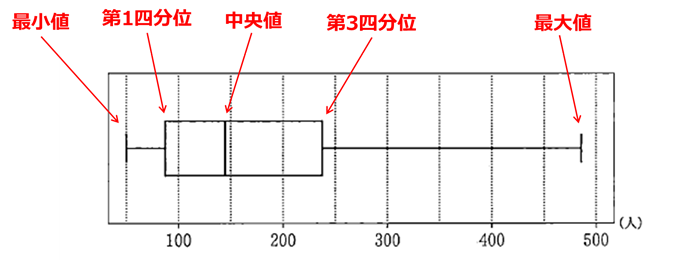
となります。
問題の4つの散布図は
横軸:教育機関1機関あたりの学習者数
縦軸:教員1人あたりの学習者数
ですが、横軸の最大値は、箱ひげ図をみると「450~499人」ですので、まず①の散布図は違うことが分かります。
「最小値」や「中央値」などは参考にならないようですので、次は縦軸について、図4のヒストグラムと見比べてみます。
例えば、「15~29人」は11か国、「30~44人」は6か国といった具合に、それぞれの階級に含まれるプロットの数を丁寧に数えていくと、
箱ひげ図に当てはまる散布図を見つける「セ」の答えは②
問(3)
続いて(3)に進みます。
この問題は、相関係数の求め方が
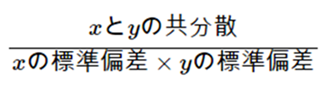
という公式さえ知っていれば、問題文にいろいろ出てくる数字は関係なく、表1から答えは簡単に導けます。
735.3/(81.8)×(72.9)=0.63
一の位の数字「ソ」の答えは⓪、小数第一位の数字「タ」の答えは⑥、小数第二位の数字「チ」の答えは③
問(4)
最後の(4)は(3)で求めた相関係数を参考にして当てはまる散布図を選ぶ問題です。
前問の表1で
Sの平均値: 81.8
Tの平均値: 72.9
ということが示されています。
4つの散布図をよく眺めてみると、⓪と①の平均値は上記より明らかに高いと思われるので除外します。
また、前問で求めたSとTの相関係数は「0.63」でした。
一般的な目安として、相関係数の値は
0.7~1.0 : 強い相関がある
0.4~0.7: 相関がある
0.2~0.4: 弱い相関がある
0.0~0.2: ほとんど相関がない
とされており、「0.63」というのは割と強い相関があるといえます。
残りの散布図②と③のうち、②はバラつきが大きく相関が高いとはいえません。
従って、当てはまる散布図を選ぶ「ツ」の答えは③
統計というのは一般的な数学のイメージとは異なるかと思います。
それにしても今年の問題は計算力よりも視力や根気強さが求められる内容でした。
【次はこちらもおすすめ】





