共通テストの統計の問題は公式など知らなくても誰でも解けます
1月16、17日の2日間、大学入学共通テストが行われました。
今回は大学入試センター試験に代わって初めての実施ですし、コロナ禍での試験ということで、受験生はもちろん運営側も例年以上の緊張を強いられたかと思いますが、特に大きな混乱もなく無事に終えられて何よりでした。
さて、共通テストは、思考力・判断力・表現力を重視する出題内容になるとのことで、日頃データ分析を行っている市場調査会社のリサーチャーとしては、特に数学の統計問題の内容が気になるところです。
大学入試の数学の問題というと少し難しい印象があるかもしれませんが、共通テストの統計に関する問題は、特に計算の必要はありませんし、公式の知識などがなくても誰でも解けますので、皆さんもぜひ挑戦してみてください。
今年の問題を解いてみる
共通テストの問題は、新聞各社や予備校などのサイトに掲載されていますので、「共通テスト 2021 問題」で検索して、「数学Ⅰ・数学A」の問題をご覧になってみてください。
数学Ⅰ・数学Aの第2問に統計に関する問題があります。
問題(3)は第1次産業(農業、林業と漁業)、第2次産業(鉱業、建設業と製造業)、第3次産業(前記以外の産業)の都道府県別の就業者数割合について、2つずつ組み合わせて散布図に示したものを1975年度と2015年度で比較し、それに関する記述の正誤を答えさせる問題です。
問題文中に、「相関が強くなった」とは、相関係数の絶対値が大きくなったことを意味する、とあるのですが、相関係数は−1以上1以下の値をとり、絶対値が1に近いほど相関が強く、0だと無相関ということになります。
これを散布図で示すと、一方が上がるともう一方も上がる「正の相関(r=1)」、一方が上がるともう一方は下がる「負の相関(r=-1)」は、それぞれ以下のような形になります。
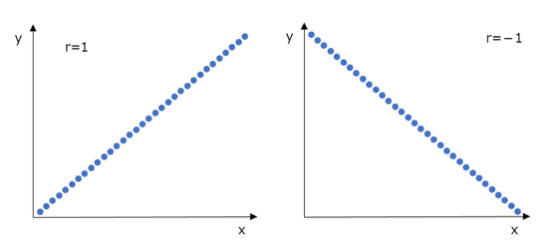
すなわち、散布図の形状は、正負いずれにしろ相関が強いほど直線に近くなるわけです。
問題では、1975年度を基準としたとき2015年度の方がより直線的な関係になっていれば「相関は強くなった」と言えるわけです。
数学の他の問題は、公式や定理の知識が必須だったり、計算量が多かったりしますし、全体としての難易度は決して低くありませんが、こと統計に関する問題は拍子抜けするほど簡単と思われたのではないでしょうか。
さらにモデル問題を解いてみる
これだけでは少し物足りないという方もいるかもしれませんので、本試験に先立って平成29年に公開されたモデル問題もみてみることにしましょう。

出典:大学入試センター「大学入学共通テスト」マークシート式問題のモデル問題例(平成29年7月)
太郎さんと花子さんは、東北地方で一日の平均睡眠時間が長い県が多い理由を考え、
東北地方は平均気温が低い
↓
一年間の平均気温が低い都道府県ほど睡眠時間が長い傾向がある
という仮説を立てたわけですが、表にある8県のみの平均気温と47都道府県全体の平均とを比較しただけでは、仮説が正しいとする根拠としては不十分で、他の都道府県についても調べてみなければならない、というわけです【問題(1)の解答は②】。
出典:大学入試センター「大学入学共通テスト」マークシート式問題のモデル問題例(平成29年7月)
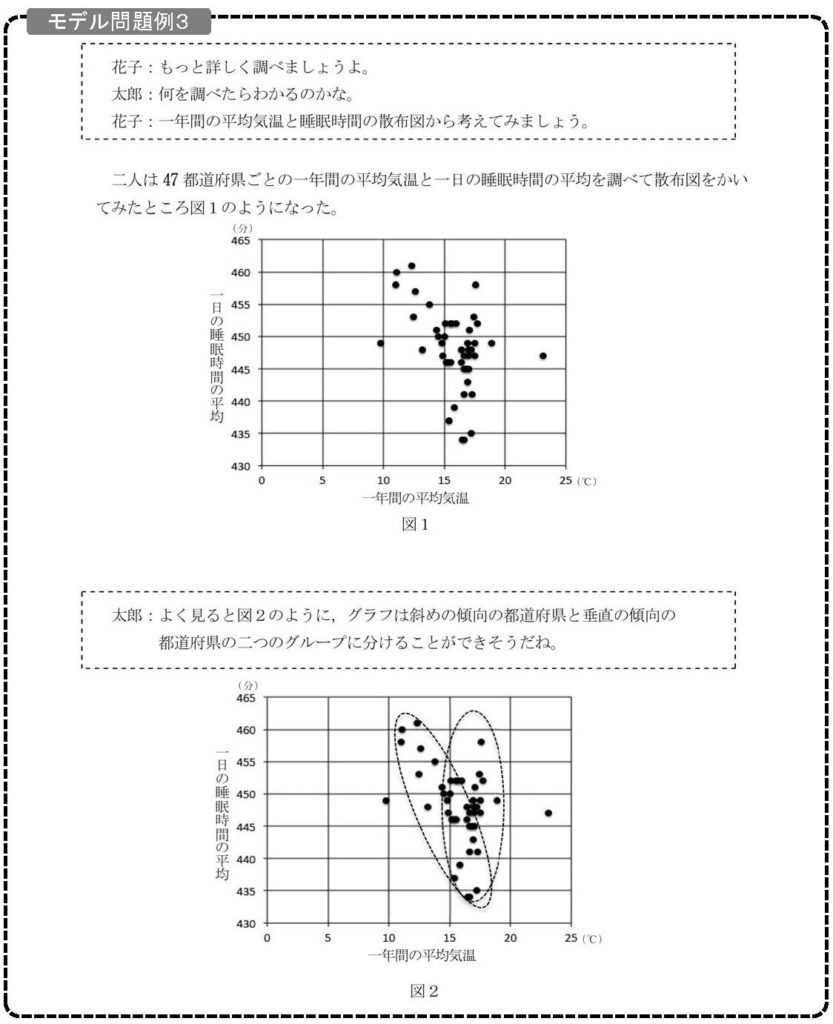
太郎さんと花子さんは、47都道府県すべての一年間の平均気温と一日の平均睡眠時間を調べて、散布図をかいてみました(図1)。
問(2)は、図1をみて相関係数に「最も近いもの」を選ばせる問題ですが、相関係数を計算で求めさせるのではなく、散布図の形状から推測させる問題となっています。
相関係数(r)の求め方は、

数式で表すと
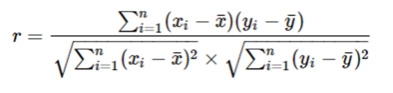
となります。
式の意味はともかく、非常に計算が面倒そうというのは誰もがお感じになるでしょう。
もし、47都道府県すべての平均気温と睡眠時間のデータが載せられて、そこから相関係数を手計算するとしたら、恐らくそれだけで試験時間が終わってしまいます。
相関係数は表計算ソフトで簡単に算出できるわけですし、実社会で必要なのは厳密な公式の理解や計算過程よりも、大まかでも結果を正しく解釈できるようになること、という出題意図なのでしょう。
問題の図1をみると、どちらかというと右肩下がりの負の相関(平均気温が高くなると睡眠時間が短くなる)ですが、あまり大きな相関はない、ということになります【問題(2)の解答は②】。
さらに、太郎さんと花子さんは図1の散布図をよく見て、47都道府県すべて合わせて考えるのではなく、右肩下がりの斜めの(負の相関が強い)傾向の都道府県と、垂直の(ほとんど相関がない)傾向の都道府県の二つのグループに分けた方がよいのでは、と気づきます。
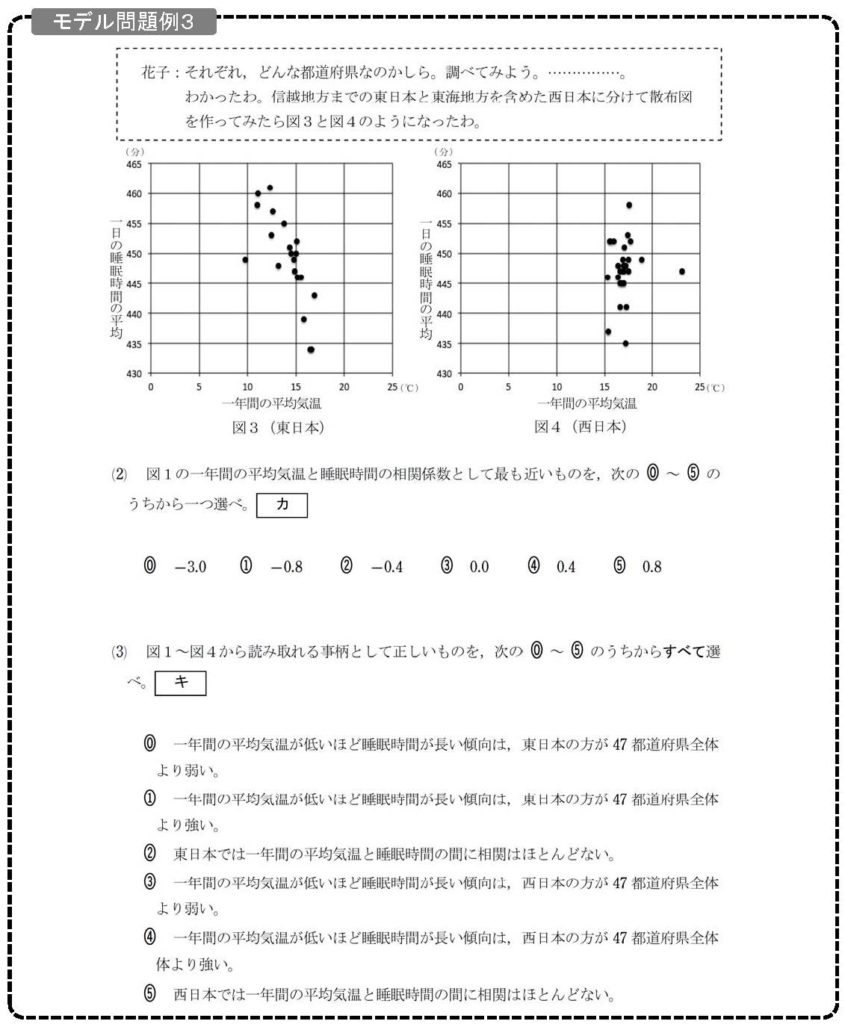
そして、それぞれのプロットがどの都道府県にあたるかを調べてみた結果、信越地方までの東日本(図3)と、東海地方を含めた西日本(図4)の二つに分けられた、というわけです。
図1の散布図を見て二つのセグメントに分けた方がよいと見抜く、というのは相当センスがよいと思います。私だったら気づかないかもしれません・・・
ともかく、東日本では平均気温が低いほど睡眠時間が長い傾向があるが、西日本では両者の間にほとんど相関がない、ということが見えてきました。
そこで、問題(3)ですが、こちらは正しい選択肢をすべて答えさせる、つまり正解がいくつかは分からないところもポイントです。ただ、⓪と③、①と④、②と⑤が対になっていますので、それぞれどちらかが正しく、正解は3つと考えられるでしょうか【問題(3)の解答は①、③、⑤】。
社会人に求められる統計スキル
本試験の問題に比べると少し歯ごたえがありますが、やはり特に数式の知識や計算は必要ありません。
数学、特に確率・統計に関してはほとんど学習内容を覚えていないという方も多いかもしれませんが、一般常識的な統計リテラシーで問題なく解けたのではないかと思います。
実は、問題にはまだ続きがあり「平均気温の他に、睡眠時間の長短に影響する要因はないか?」ということで、都道府県別に一日の仕事時間や通勤・通学時間の平均などを調べていったりします。
数学の試験問題としてはややしつこいくらいに長いのですが、データ分析に臨む姿勢として私たちが教えられるところもあります。
社会人に求められる統計スキルも、単なる計算・データ処理能力ではなく、納得いく結果が出るまで地味な計算・データ処理の手間を惜しまない粘り強さ、そして、それ以上に、アウトプットの正しい解釈であり、データの海から課題を発見し、仮説を構築し、適切に検証できる能力でしょう。
【次はこちらもおすすめ】