データ分析の手法はたくさんありますが、その中で最も活用されているものの一つは「相関」ではないでしょうか。2種類のデータの関係を相関係数という一つの値に集約できるのが魅力ですが、Excelなどの表計算ソフトで簡単に求められますし、何よりもアウトプットの意味が誰にでもわかりやすいのが重宝される理由でしょう。
相関係数は−1以上1以下の値をとり、絶対値が1に近いほど相関が強く、0だと無相関ということになります。
一般的な目安としては、相関係数(r)の絶対値によって
|r|=0.7~1.0 強い相関がある
|r|=0.4~0.7 相関がある
|r|=0.2~0.4 弱い相関がある
|r|=0.0~0.2 ほとんど相関がない
とされています。
とても使い勝手のよい相関ですが、たまにあまり適切といえない使い方、見方がされているように見受けられることもあります。
今回は、相関を見る際の注意点をいくつかあげてみましょう。
注意点(1) まず、データの性質を確認しましょう
2変量のデータ形式が整っていれば、とりあえず相関は出せます。
ただ、データの性質によって相関の求め方が異なります。
データの性質は、以下の4つの尺度にまとめられます。
①名義尺度
他と区別し、分類するためだけのデータ。
例えば、アンケートで住所(都道府県)を聞く場合に
北海道
青森県
岩手県
:
等とコードが振られていたりしますが、この「1」「2」「3」・・・は便宜的なもので、数値間に大小関係があるわけではなく、順序にも特に意味はありません。
②順序尺度
数値の大小関係はあるが、数値の間隔は同じとはいえないデータ。
例えば、商品テストのアンケートで「1位」「2位」「3位」と好みのランキングを聞く場合、順序には意味があるものの、「1位」と「2位」、「2位」と「3位」の間の好みの程度の違いが同じとはいえません。
③間隔尺度
大小関係に加え、数値の間隔も同じ(とみなされる)値。
例えば、気温や西暦(和暦)などが当てはまります。また、アンケートでよく使われる段階的な評価(「5.非常によい」~「1.まったくよくない」など)も、数値の間隔は同じとみなして間隔尺度として用いられることが多いです。
間隔尺度については平均や標準偏差といった統計量が使えます。
④比例尺度
大小関係や数値の間隔だけでなく、間隔の比率にも意味がある値。
例えば、身長、体重、年収、時間などが当てはまります。間隔尺度とは異なり、体重100kgの人は50kgの人の倍の重さ、といった計算が可能です。
相関というと、通常はピアソンの積率相関係数のこと(Excelで「correl」の関数で求められるのがコレです)でしょうが、ピアソンの積率相関係数が使えるのは、データが③間隔尺度、④比例尺度の場合です。
①名義尺度や②順位尺度のデータについてピアソンの積率相関係数を適用するのは適切ではなく、それでも相関を見たいという場合には、スピアマンの順位相関係数やケンドールの順位相関係数といった別の方法を用いる必要があります。
相関を求める際には、データの性質を確認した上で、適切な算出方法を使いましょう。
注意点(2) 外れ値をチェックしましょう
まず、下図をご覧ください。
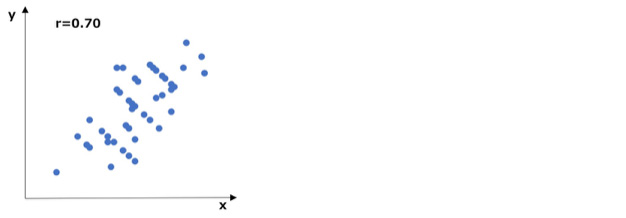
こちらは、ある2変量x、yのデータを散布図で表したものです。
一方が増えればもう一方も増えるという概ね正の相関がみられ、相関係数は0.70となっています。
一般的な目安としては「強い相関がある」ということになります。
では、次に下図をご覧ください。
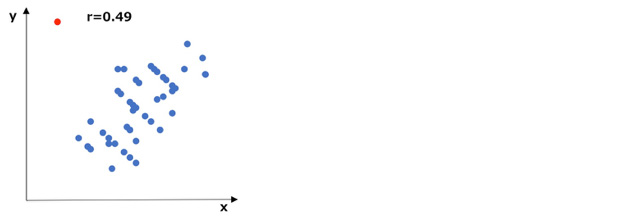
先ほどのデータの中に一つだけ極端な値(外れ値)が入っているものです(赤点)。
たった一つの外れ値があるだけで相関係数が0.49と随分と下がってしまいます。
こういう場合は、外れ値を除いたデータで相関を見るべきでしょう。
上記は外れ値のせいで相関が下がってしまうケースですが、逆に外れ値があることで見かけの相関が上がってしまうパターンもありえます。
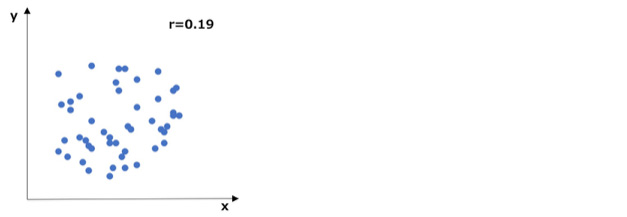
こちらはデータ分布がバラバラで規則性がなく、相関係数も0.19と「ほとんど相関がない」状況です。
ただ、一つの外れ値が入ることにより、下図のように相関が0.35と「弱い相関がある」に変化してしまいます。
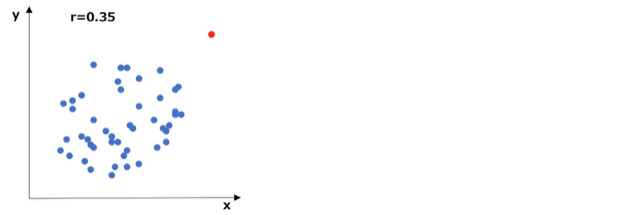
つまり、相関は外れ値の影響が強く出てしまう性質があるのです。
このことは相関係数の求め方から理解できます。
相関係数(r)は、以下の式で求められます。

「共分散」とは、対応する2組のデータ(x、y)について平均との差(偏差)を出し、それらを掛け合わせたものの平均のことです。
なぜ、標準偏差の積で割るのかというと、例えば「身長」と「体重」など単位の異なるデータを扱う場合でも、共通指標として相関をみることができるようにするための操作です。
外れ値があると偏差の積でブレが増幅されてしまいますので、共分散、ひいては相関係数の値に大きく影響してしまうわけです。
外れ値の有無はデータ上でも簡単にチェックできますし、相関を出す際には確認するよう心掛けましょう。
注意点(3) 散布図を描きましょう
外れ値を除いたデータで正しい方法で相関を求めれば、算出された係数だけを見て相関の有無を判断してよいのでしょうか。
いえ、もう少しだけ慎重になりましょう。
<相関が高い場合に確認したいこと>
「かき氷の販売数」と「海での水難事故数」の相関が高かったとしましょう。ただ、この場合は両者に直接的な関係があるというよりも、「気温が高い」から「かき氷が売れる」「海水浴に行く人が多く、事故も増える」と考えるのが妥当でしょう。
このように、ある2つの事象に隠れた別の要因によって、あたかも両者に相関があるようにみえることを「疑似相関」と言います。
隠れた要因(上記例の場合は「気温」)に見当がついている場合は、その要因の影響を除いた形で相関を求める(「偏相関係数」といいます)ことが可能です。
相関が高い場合には、因果関係にもある程度納得できるかどうか、もしかしたら疑似相関でないかどうか、と考えてみるようにしましょう。
<相関が低い場合に確認したいこと>
下図をご覧ください。
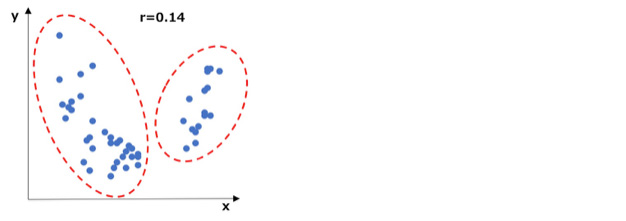
こちらのデータ分布は、全体だと相関係数が0.14で「ほとんど相関がない」ことになります。
ただ、まったくバラバラな分布なのではなく、2つの赤丸で囲んだグループで分けてみると、それぞれのグループ内では相関関係がありそうです。
このような場合は、全体で相関を見るのではなく、複数のセグメントに分けて分析すべきでしょう。
次に、下図をご覧ください。
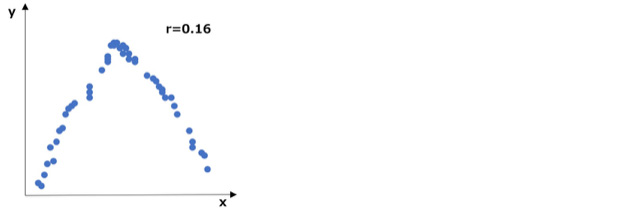
こちらも、全体だと相関係数が0.16と低い値となっています。
ただ、明らかに規則性がみられますね。例えば、気温・室温と生産性の関係(暑すぎても寒すぎても活動量や集中力が落ちる)といったケースが当てはまるでしょうか。
上記の2例は、いずれも相関係数だけでは見落としかねない、散布図を見ることによって浮かび上がる関係性もある、ということを示しています。
多少手間ですが、相関を見る際はできるだけ散布図も確認するようにしましょう。
散布図は外れ値のチェックにもなりますし、相関係数という数値だけに頼らずデータ分布を視覚的に把握することにより、分析にも深みが出てくるでしょう。
いかがでしょうか。手軽な分析手法と思われる相関ですが、正しく活用してアウトプットを適切に解釈するのはそれほど簡単ではないと思いますよ。
【次はこちらもおすすめ】





