統計的データ活用思考法第3回目の今回は、迷惑メールフィルタリングから自動翻訳、ロケット制御にいたるまで、現代社会で幅広く応用されているベイズ理論について、その基本的な考え方を簡単にご紹介します。
ある就職情報サイトが、内定辞退率の予測データを企業に販売していたニュースを覚えていますか?
就職活動中の学生のサイト内行動履歴から内定辞退率を判定し、企業側に販売した問題でしたね。
いつの間にか自分の知らないところで個人データが利用されて、自分の人生を左右しかねないような判断が勝手になされてしまうのではないかと思うと、ものすごく不安になります。
※本人の同意なく個人情報(サイト上の行動ログを含む)を第三者に提供することは法律で禁じられています。
内定辞退率の予測
ところで、内定辞退率はどのように予測できるのでしょうか。
非常にシンプルに、例えば
・ある企業の内定辞退率は毎年10%前後
・就職情報サイト内で、ある特定のページを閲覧する人は、内定辞退者なら約9割、辞退しない人だと2割くらい
という状況を考えてみましょう。
まず、何も情報がない場合だと、ある人が「内定を辞退する確率」は例年通り10%程度と推定するしかありません。
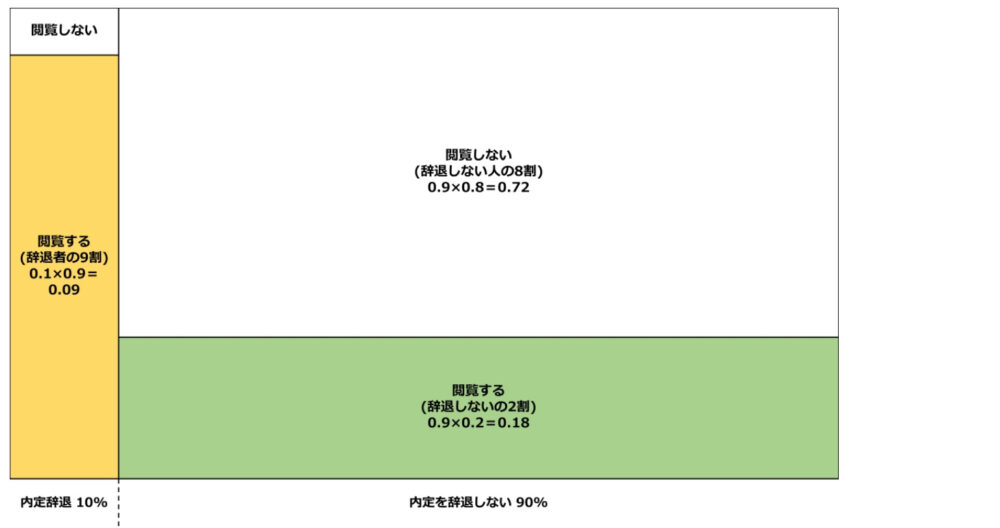
しかし、もしこの人が「内定辞退者がよく閲覧するページを見た」という情報が加わると、下図の色付き部分
内定辞退者でページを閲覧する人: 0.1×0.9=0.09 (9%)
内定を辞退しないでページを閲覧する人: 0.9×0.2=0.18 (18%)
のケースに限られることになり、内定辞退の確率は
0.09/0.09+0.18=33.33333・・・ (33%)
と、当初の確率(10%)の3倍以上となります。
条件が一つだけでは不十分ですが、たくさん条件を増やして精度を高めていけば、情報が欲しい企業に販売できるレベルの信頼できる予測データになるかもしれません。
これはベイズ推定の応用例といえます。
ベイズ推定
ベイズ推定とは、ベイズの定理をもとに、事後的に得られた情報によってもとの確率(事前確率)を補正していく(ベイズ更新)ことです。
【ベイズの定理】
P(B) = 事象Aが起きる前の事象Bの確率<事前確率>
P(A) = 事象Aが起きる確率
P(A|B) = 事象Bが起きた場合の事象Aの確率<尤度(ゆうど)>
P(B|A) = 事象Aが起きた後での事象Bの確率<事後確率、条件付き確率>
先程の例に当てはめると
P(B) = サイト閲覧状況がわかる前の内定辞退率:10%
P(A) = 特定ページを見る確率 (上図の色付き部分):9%+18%=27%
P(A|B) = 内定辞退者のうち、特定ページを見る確率:90%
P(B|A) = 特定ページを見た人が内定を辞退する確率:33.33333・・・%
となります。
曖昧さが特徴
ベイズの定理は18世紀中頃に発表されましたが、事前確率に人の主観的な判断を認める曖昧さ(事前確率がわからない場合は、とりあえず50%などと設定しておいてもよい)が批判されるなど、しばらく統計学の世界では異端視されてきました。
近年、コンピュータの処理能力が向上し、ビッグデータでもベイズ更新が瞬時に行えるようになると実用的なレベルまで精度が上がり、融通の利く曖昧さはむしろ利点と評価されるようになってきました。
現在では迷惑メールのフィルタリング、音声・画像認識や自動翻訳、与信管理、犯罪捜査、医療診断、ロケットの軌道制御などまで、私たちの身の回りで幅広く応用されています。
【次はこちらもおすすめ】





