多人数で物事を決める際、話し合いによって全員一致に至れば申し分ないですが、どうしても意見が分かれる場合、最もポピュラーな決定方法は多数決かと思います。
ただし、多数決で決まったからといって、少数派の納得を得る努力を怠れば、対立を深めるだけで多数決前より状況が悪化することになりかねませんし、そもそも多数決が本当に多数派の意思を反映するのかどうかも考えてみる必要があります。
例えば、X、Y、Zの3人が立候補した選挙で、10人の有権者に
○:好き
△:どちらでもない
×:嫌い
をつけてもらう形で投票してもらった結果が以下の通りだったとします。
○(好き)の多数決で選ぶとすると、「X」が4票獲得で当選となりますね。
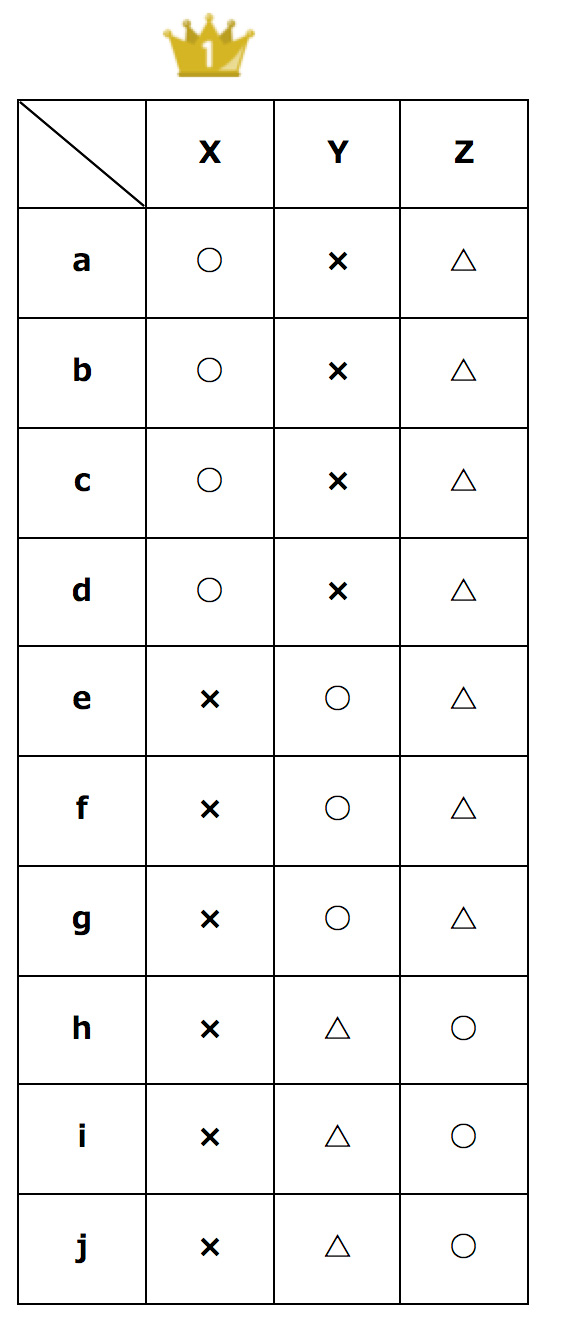
ただ、よく見ると、「X」は○(好き)をつけた人以外は全員×(嫌い)としており、有権者の好き嫌いが極端に分かれる候補のようです。逆に、「Z」は×(嫌い)が1人もいません。このように、○(好き)の数では最多得票でも、過半数が不支持といった場合、有権者の民意が正しく反映されているといえるでしょうか。
もし、X、Y、Zの3人による争いではなく、「XとY」あるいは「XとZ」の一騎打ちになった場合どういう結果になるか考えてみましょう。このケースでは△(どちらでもない)はなくなり、○(好き)か×(嫌い)かのみの判断となります。
「XとY」の対戦だと、「Z」に○(好き)をつけていた3人は「X」よりも「Y」を選ぶでしょうから、○(好き)の数は、X:4人、Y:6人、となって「Y」が勝ちます。
同様に、「XとZ」の場合も「Z」の勝利となり、もし一騎打ちだったら「X」は「Y」にも「Z」にも勝てなかったことになります。一対一なら劣勢でも、3人の選挙になれば「Y」と「Z」で○(好き)が分かれると多数決なら勝ってしまう“投票のパラドクス”が生じることがあるのですね。
このように、多数決ルールは、選択肢が増えると票の割れに弱い、不支持の度合いを反映しにくい、等といった弱点が指摘されています。そして、多数決に変わる投票ルールもさまざま考えられてきました。その一例が「ボルダルール」です。
ボルダルールは、例えば立候補者が3人の場合、先ほどの例のような○(好き)、△(どちらでもない)、×(嫌い)、ではなく
1位:3点
2位:2点
3位:1点
と点数をつけ、その総得点により順位づけをします。
ちなみに、先ほどの投票結果をボルダルールで見直してみると、総得点が最も高いのは「Z」で、「X」は最下位となります。
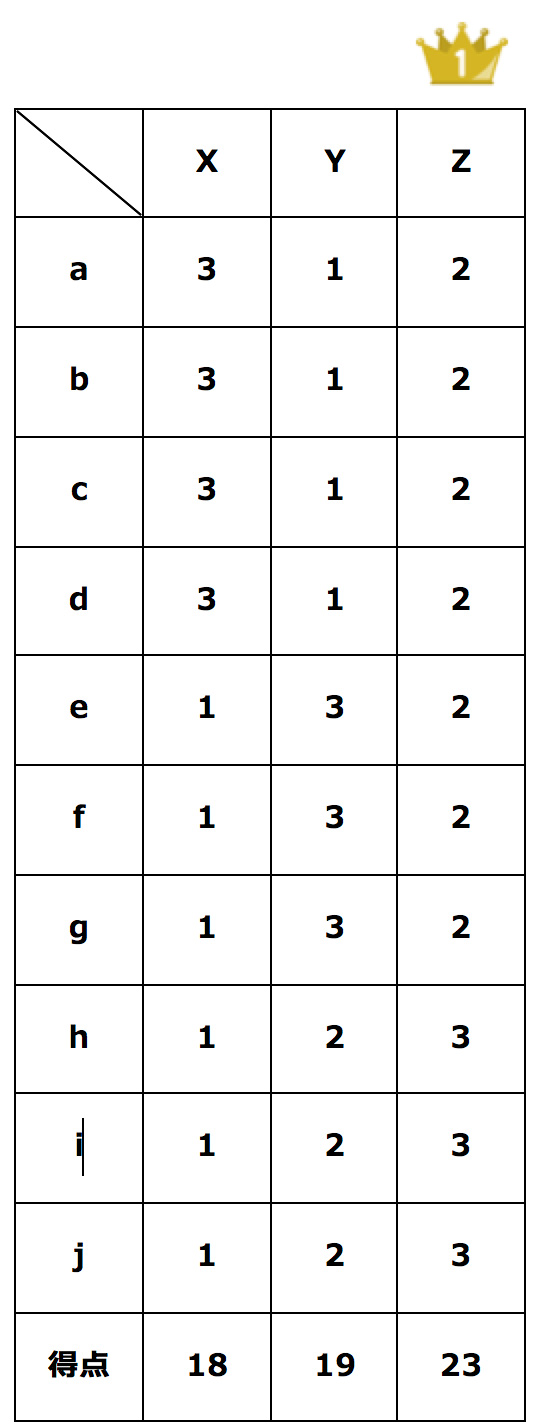
ボルダルールだと、不支持(=低得点)を加味することで、支持の偏った候補ではなく、より幅広い層に受け入れられる候補を選出することが可能になります。
ただ、投票や集計の負担などを考えると、実際問題としては単純明快な多数決が採用されるケースが多いでしょうし、そもそも他にどんなに優れた投票ルールが考案されたとしても、(選択肢が3つ以上ある場合)一人一人の選好を完全に反映させる集団的な意思決定方法は存在しえない(「アローの不可能性定理」)と考えられています。
投票ルールの欠陥は民主主義の限界なのでしょうか。「民主主義は最悪の政治体制~」というチャーチルの言葉ではないですが、常に改善を模索しながらも永遠に最善にたどり着けないのが民主主義の最も優れた点なのかもしれません。不完全だからこそ投票結果を絶対視しないバランス感覚が求められる、と考えれば、誰もが従わざるをえない完璧な民主主義が実現するよりもむしろ望ましいかとも思われます。
【次はこちらもおすすめ】