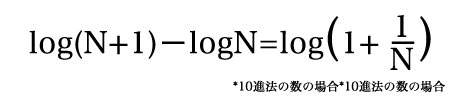新聞を見ると、日付や天気予報(降水確率や最高・最低気温)、内閣支持率などの世論調査、企業業績や株価・為替相場などの経済指標、スポーツの記録や宝くじの当選番号など、紙面にはさまざまな種類の数字が載っています。
これらの数字だけピックアップして分布を調べてみたらどうなるでしょうか。
新聞紙上の数字だけでなく、川の長さや面積、あるいは人口や公共料金の請求額などといった幅広い自然・社会現象でみられる数字は、1から始まる数が最も多く、先頭の数の分布には一定の規則性があることがわかっており、ベンフォードの法則とよばれています。
Nから始まる数字の出現確率は
で、エクセルの関数式で簡単に求められます。
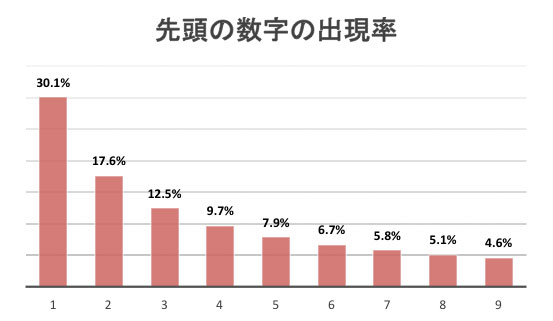
N=1の場合はlog(2)=0.301029…ですので、1から始まる数の出現確率は30.1%となります。同様に9までの分布は以下の通りとなり、1または2から始まる数字だけで半分近くに達することがわかります。頭で考えるともう少し均等に分布していそうにも思いますが、日常で目にする数字を思い浮かべると何となく納得できる気もしますね。
なお、電話番号のように決まった桁数で割り当てられた数字や、経費の上限が定められた中での精算額など上限・下限が決められた範囲における分布には当てはまりません。
ちなみに、平成27年国勢調査の速報集計で全国市区町村の人口分布をみてみると
先頭の数字
「1」・・・・・ 30.2%
「2」・・・・・ 15.7%
「3」・・・・・ 13.4%
「4」・・・・・ 9.8%
「5」・・・・・ 7.9%
「6」・・・・・ 6.2%
「7」・・・・・ 6.7%
「8」・・・・・ 5.4%
「9」・・・・・ 4.6%
と、ほぼベンフォード則に従っているようです。
この法則は、例えば帳簿や領収書の金額、あるいは投票結果や実験データの数値などが異様に1から始まる数字が多い(少ない)等といった場合には人為的な改ざんが加えられた可能性があると考えられ、不正検出にも応用することができます。
【次はこちらもおすすめ】