サンプルサイズとサンプル数の違い
アンケート/市場調査を実施する際に、「いったい何人くらいに協力してもらう必要があるのか?」とお悩みの方が多いものと思います。
これをリサーチ用語で表現すると「どのくらいのサンプルサイズが必要になるのか?」となるわけですが、「サンプルサイズ」のところを「サンプル数」という人も結構多いですね。
統計学の本では、母集団から取り出した(=サンプリングした)データの集まりが「サンプル(標本)」で、「サンプル」に含まれるデータの個数が「サンプルサイズ(標本の大きさ)」であると説明されています。
このコラムでは、正しい用語として「サンプルサイズ」の表記を用いていますが、「サンプル数」のほうがしっくりとくるようでしたら、そのように読み替えてください。
本コラムは、「調査の準備~運用~分析~活用」まで、はじめての方にもわかりやすく解説した実務者向けシリーズ(全4回)の一編です。他のコラムもあわせてぜひご覧ください。
【同シリーズのコラム】
さて、サンプルサイズは、調査結果の精度を左右する要素ですが、このくらいあれば大丈夫という頃合いを見極めるのはとても難しいテーマです。
有効回答数が少なすぎると誤差が大きくなってしまいます。
かといって、大規模な調査をしようとすると、費用がかさんでしまいます。
しかし、これは結構ぜいたくな悩みでもあります。
今日のようにインターネット調査が一般的に実施されるようになる前は訪問面接調査や会場調査が主流で、ちょっとした調査をしようとすると少なくとも100万円、200万円はかかるというのが当たり前でした。当時は、結構大手の企業でもn=50人のアンケートの結果をもって意思決定をするということも珍しくはありませんでした。
以前に比べると、インターネット調査の普及により、予算による制約は随分と改善されてきていますので、今はその分「誤差」の方にこだわって検討することができます。
そこで、まずはサンプルサイズに関する基礎知識や理論的な内容を説明し、そのうえで統計学的に信頼に足る調査結果を得るために必要なサンプルサイズを決める考え方について紹介します。このページの最後に、アンケートの担当になった方に便利に使っていただけるエクセルファイルで作成したサンプルサイズ計算ツール(ダウンロード無料)へのリンクを掲載しておきますので、あわせてご利用ください。
ポイントその① 無作為抽出
テレビや新聞などで内閣支持率が上がった/下がったというニュースが流れる時に、無作為抽出という言葉を聞いたことがありませんか。
報道各社から発表される内閣支持率や政党支持率の多くはRDD方式による電話調査で実施されています。
「RDD」とは「ランダム・デジット・ダイヤリング(Random Digit Dialing)」の略で、コンピューターで無作為に選んだ番号に電話をかけて調査する方法です。近年は固定電話を持たない世帯も増えていますので、地域を限定しない全国規模の調査の場合、最近では固定電話だけでなく携帯電話も対象に含めるようになってきています。
このように、調査対象者をできるだけ無作為に抽出することで有権者の母集団における代表性を高めるようにしているわけです。
では、どの程度の調査対象(標本)を集めれば信頼できる結果と考えられるのでしょうか。
ポイントその② 中心極限定理
世論調査などサンプル調査の信頼性の根拠に「中心極限定理」があります。
簡単に説明すると、「無作為に抽出した標本の大きさが十分に大きければ、母集団データがどのような確率分布であっても、(ほとんどの場合)標本平均の分布は母集団の真の平均を中心とした正規分布に従う」ということです。
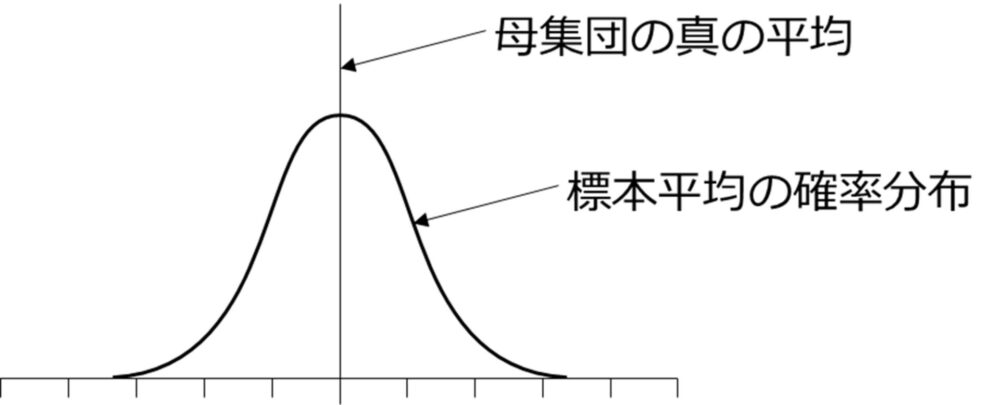
母集団の分布は正規分布でなくても、そこから無作為に抽出した標本の平均をプロットすると正規分布に近づくというところがミソです。標本平均が正規分布なのであれば、母集団の真の平均からの誤差について確率的な推計が可能になり、サンプル調査でもある程度の幅をもって信頼できる結果が得られるわけです。
そして、どの程度の標本誤差を許容するかによって必要なサンプルサイズも決まってきます。
ポイントその③ 標本誤差
標本誤差は、一般的な95%信頼度(100回調査を行えば95回は同様の結果が得られると想定)では以下の値以下に収まります。
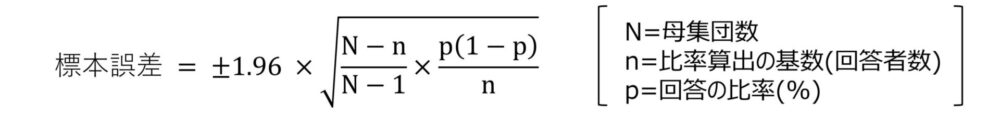
なお、
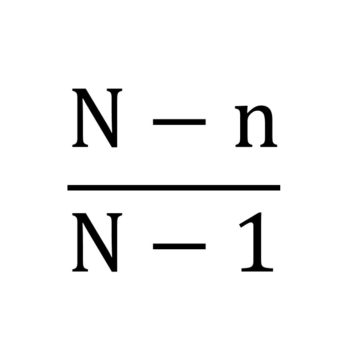
の部分は、母集団がサンプルサイズに比べ十分に大きければ「1」とし
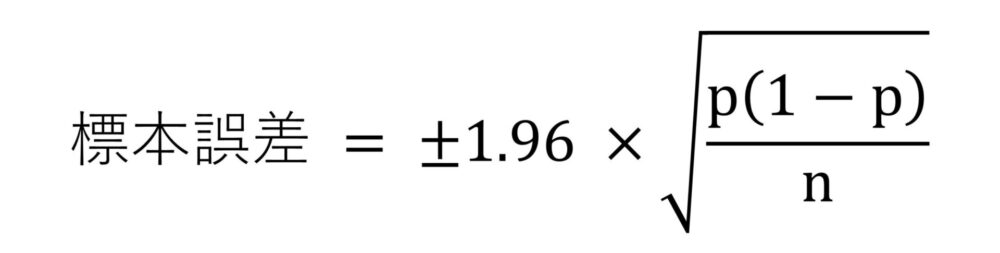
として差し支えないでしょう。
標本誤差と必要サンプルサイズ
上の式を見ても分かる通り、標本誤差は回答比率が50%(p=0.5)の時に最も大きくなります。どちらに転ぶかわからない半々の状態が最も判断が難しいわけです。
p=0.5とした場合、サンプルサイズの違いによる最大誤差は以下のようになります。

サンプルサイズが10,000人であれば、ある質問に対する回答割合が50%の場合、誤差は±1.0%ですので、母集団における真の値は49.0%~51.0%と推定できますが、サンプルサイズが100人だと誤差は10%近くになると考える必要があるわけです。
そして、今度は、許容できる標本誤差を設定した上でサンプルサイズを決める場合、たとえばp=0.5として上の式を変換し、
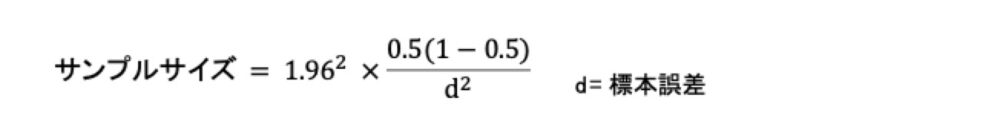
で求めることができます。

±5%まで標本誤差を認めるとサンプルサイズは384人で済みますが、±2.5%にすると1,537人が必要となります。
標本誤差はnの二乗根に反比例するので、標本誤差を半分にするためにはサンプルサイズを4倍にしなければならないわけです。
標本誤差早見表
一般的な95%信頼度での誤差を表にまとめたものが以下の標本誤差早見表です。
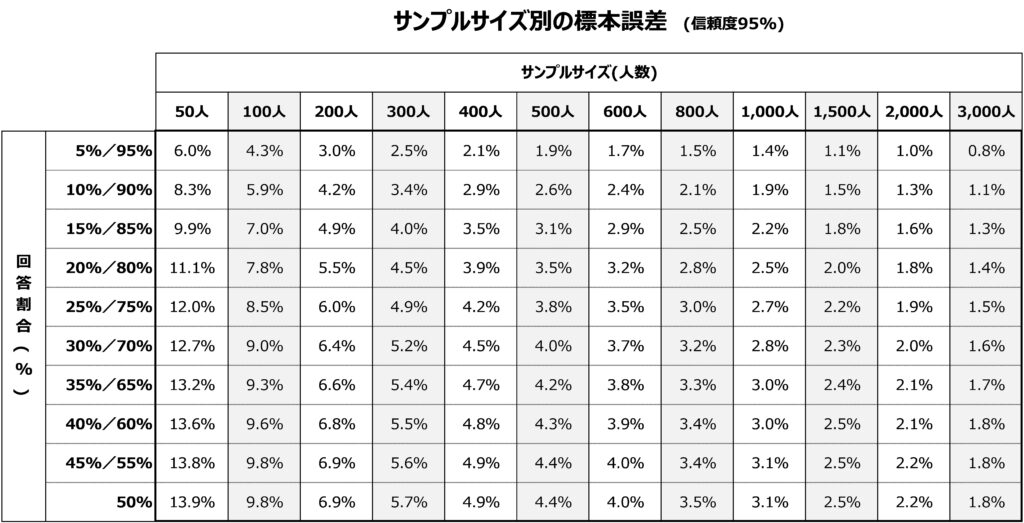
たとえば、全国500人の男女を無作為に抽出し、商品Aを「知っている」と回答した割合が70%だった場合、「サンプルサイズ(人数)」が「500人」の列と「回答割合(%)」が「30%/70%」の行とが交差するところを見ると、誤差は「±4.0%」となります。従って、商品Aの認知度は70%±4.0%で66~74%の範囲と考えられます。
許容できる誤差は±5%まで、あるいは±10%までとするケースが多いようですので、±5%の誤差で必要とされるサンプルサイズについて、テレビ視聴率と内閣支持率の例でみてみましょう。
テレビの世帯視聴率
最近、テレビの世帯視聴率は1ケタの番組も多いようですし、上の表で回答割合(この場合は視聴率)が10%から15%あたりまでで誤差が5%以下になるサンプルサイズを探せばよいでしょう。
そうすると、視聴率調査に必要なサンプルサイズは200世帯程度でもよいことになります。とはいえ、誤差が5%なら視聴率がコンマ何ポイント上がった/下がったと一喜一憂するのはおかしいですね。
内閣支持率
一方、内閣支持率は調査主体によって数字に差があるものの、最近は5割前後で推移する傾向があります。回答割合が50%で誤差が5%となると、必要なサンプルサイズは400人で、先程の視聴率調査の倍近い人数になります。
サンプルサイズ(人数)の目安は「100人」「400人」など
通常のアンケート調査では事前に回答割合を想定できないケースがほとんどでしょう。
そういうときは誤差が最も大きい50%の回答割合でサンプルサイズを考えてみます。
すると
誤差が±10% ⇒ 100人
±7% ⇒ 200人
±6% ⇒ 300人
±5% ⇒ 400人
±4% ⇒ 600人
±3% ⇒ 1,000人
といったことがわかります。
「100人」「400人」「600人」さらに精度を高めたければ「1,000人」といったあたりが、許容する誤差に基づいてサンプルサイズを決める目安となります。
サンプルサイズが100人というのは、1人=1%でわかりやすいのですが、回答割合が50%の時に±10%の誤差を認める、すなわち40~60%と幅をもった結果でも構わなければn=100でよいわけです。
ただし、全体だけでなく性別や年代別などに分けて細かく結果をみたいという場合、それぞれの集計・分析ベースの人数も考えなければなりません。
たとえば、20~69歳の男女に対して、性別や10歳刻みの各年代で人数を均等にアンケートを実施する場合、年代別の結果まで誤差が±10%以内でみられるようにしたいのであれば、各年代100人ずつ、計500人のサンプルサイズが必要になります。
さらに、「50代・男性」や「20代・女性」のような性×年代別まで細かくみたいという場合、やはりそれぞれ100人ずつに設定すると、全体のサンプルサイズは1,000人になります。
集計・分析軸を細分化していき、それぞれに必要な人数を確保しようとすると、全体のサンプルサイズがどんどん大きくなってアンケート費用もかさんでしまいます。
全体のサンプルサイズを考えつつ集計・分析軸を検討していくことが大事です。
なお、誤差の大きさはともかく、統計的には「30人」以上であれば大サンプルと同様の検定が適用可能とされています。従って、集計・分析軸の最小単位はn=30以上、できればn=50以上と考えるとよいでしょう。
【性×年代別までの集計・分析軸の例】
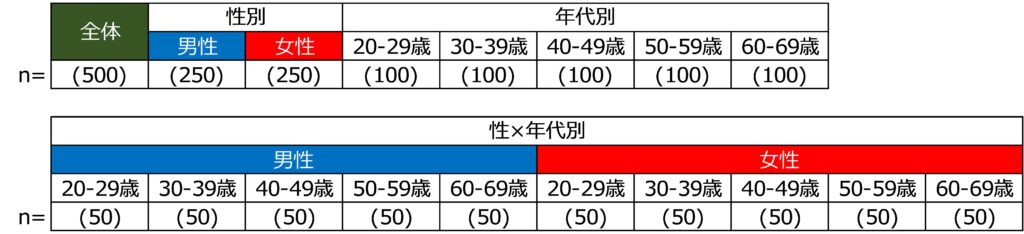
実際に調査サンプルサイズを決める際は、費用や時間のコストを勘案した上での現実的な判断が求められてきます。
サンプルサイズ計算ツール
アンケートの担当になった方用に、許容できる標本誤差などの数値を入力するだけで必要なサンプルサイズを算出する【サンプルサイズ計算ツール】をご用意していますので、ご利用ください。
以下の[ダウンロード]ボタンをクリックすると自動的にExcelファイルのダウンロードがはじまります。
信頼できる調査結果を引き出すために
適切なサンプルサイズを設定することは、調査の信頼性を確保するための基本です。しかし、実際の調査では、サンプルサイズだけでなく、設問の設計や調査対象の選定、適切な分析手法が結果に大きな影響を与えます。
当社では、調査を成功に導くためのトータルサポートを提供しています。たとえば、満足度調査については、BtoB企業向けおよびBtoC企業向けのそれぞれに特化した調査設計からデータ分析、改善提案までを一貫してサポートするサービスを展開中です。
○ BtoB企業向け
取引先企業の満足度やロイヤリティを高めるために、調査設計から結果分析、改善アクションの立案まで伴走型で支援します。業界特性に合わせた設計により、顧客の本音を引き出し、競合他社との差別化ポイントを明確にします。
詳しくはこちら>>
○ BtoC企業向け
レジャー・観光、小売、飲食などの業界に特化した調査設計で、顧客体験の全体像を把握し、ビジネス成長につながる施策の立案をサポートします。
詳しくはこちら>>
信頼できる調査結果を活かし、貴社のビジネス目標を実現するために、ぜひ当社の調査サービスをご利用ください。
お気軽にご相談ください044-271-6043営業時間 9:00 - 18:00 [ 土日祝定休 ]
ご相談・お問い合わせ【次はこちらもおすすめ】





