1/13(土)、14(日)の2日間、平成30年度の大学入試センター試験が実施されました。
高校の「数学Ⅰ」では「データの分析」が必修の学習内容となり、センター試験でも平成27年(2015年)から統計に関する問題が毎年出題されています。
分散や相関係数などの計算はExcelなどの表計算ソフトを使えば簡単に求められますが、それぞれの統計量の意味や算出方法を基礎知識として身につけておくと、実社会で出会う統計に対する理解も深まるかと思います。
そこで、今回はセンター試験の問題(「数学Ⅰ」の第4問)にチャレンジしてみることにしましょう。
センター試験の問題は、新聞各社や予備校などのサイトに掲載されていますので、「センター試験 2018 問題」で検索して、「数学Ⅰ」の問題をご覧になってみてください。
「数学Ⅰ」の第4問の最初の問題 (1)は、図から陸上選手の性別・種目別の身長分布を表すグラフを読み取る問題です。
図1のヒストグラム(度数分布図)については特に説明の必要はないでしょう。
図2の箱ひげ図は普段あまり見かけないかもしれませんが、見方は以下の通り簡単です。
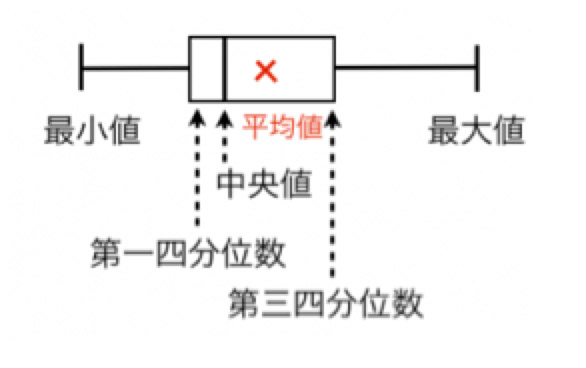
データを小さな順に並べた時に、
第1四分位数: 25パーセンタイル(全体の1/4番目の値)
第2四分位数(=「中央値」): 50パーセンタイル(全体の2/4番目=真ん中の値)
第3四分位数: 75パーセンタイル(全体の3/4番目の値)
選択肢の文中における「範囲」とは最小値から最大値までの長さ、「四分位範囲」とは第1四分位数から第3四分位数まで、すなわち箱の長さを意味します。
0.四つのグループのうちで範囲が最も大きいのは、女子短距離グループである。
⇒範囲が最も大きいのは「男子短距離」グループなので「×」
1.四つのグループのすべてにおいて、四分位範囲は12未満である。
⇒「○」
2.男子長距離グループのヒストグラムでは、度数最大の階級に中央値が入っている。
⇒度数最大の階級は「170以上175未満」、中央値は176なので「×」
3.女子長距離グループのヒストグラムでは、度数最大の階級に第1四分位数が入っている。
⇒度数最大の階級は「165以上170未満」、第1四分位数は161なので「×」
4.すべての選手の中で最も身長の高い選手は、男子長距離グループの中にいる。
⇒最も身長の高い選手は「男子短距離」グループの中にいるので「×」
5.すべての選手の中で最も身長の低い選手は、女子長距離グループの中にいる。
⇒最も身長の低い選手は「女子短距離」グループの中にいるので「×」
6.男子短距離グループの中央値と男子長距離グループの第3四分位数は、ともに180以上182未満である。
⇒「○」
正解は「1」と「6」になります。
二番目の問題(2)は、図3の散布図を見て、図4の箱ひげ図(a)~(d)がそれぞれどのグループに該当するか特定してから解く必要があります。
箱ひげ図の最大値などをヒントに、(a)~(d)のグループを見当つけると
(a):男子短距離
(b):女子短距離
(c):男子長距離
(d):女子長距離
となりそうです。
0.四つのグループのすべてにおいて、XとWには負の相関がある。
⇒散布図を見ると、すべてのグループにおいて一方の値が増えるともう一方の値も増える右肩上がりの形状で正の相関があるので「×」
1.四つのグループのうちでZの中央値が一番大きいのは、男子長距離グループである。
⇒Zの中央値が一番大きいのは「男子短距離」グループなので「×」
2.四つのグループのうちでZの範囲が最小なのは、男子長距離グループである。
⇒Zの範囲が最小なのは「女子長距離」グループなので「×」
3.四つのグループのうちでZの四分位範囲が最小なのは、男子短距離グループである。
⇒「男子短距離」グループはZの四分位範囲が最大なので「×」
4.女子長距離グループのすべてのZの値は25より小さい。
⇒「○」
5.男子長距離グループのZの箱ひげ図は(c)である。
⇒「○」
正解は「4」と「5」になります。
三番目の問題(3)は、
という公式さえ知っていれば、表1の数値から、0.754/0.200×5.36=0.7033…
で、正解は「2」とすぐに解けます。
ここで、いくつかの統計量について簡単におさらいしておきましょう。
分散:データの散らばり具合を表し、各データから平均値を引いて2乗した値を足し上げ、データ個数で割った値です。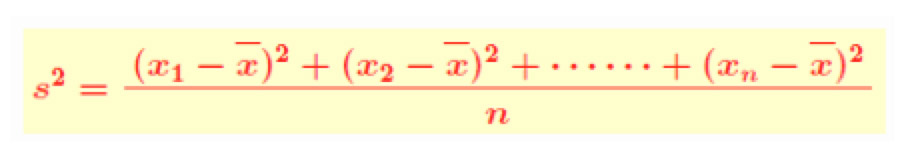
例えば、「170、165、182、173、180」という5人の身長データ(平均値=174)の分散は、
{ (170-174)2+(165-174)2+(182-174)2+(173-174)2+(180-174)2}/5=39.6
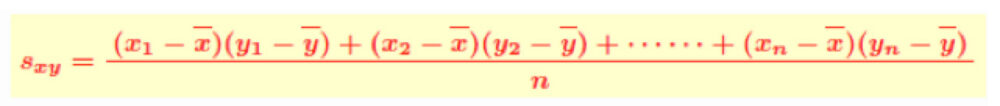
となります。
元のデータと単位を揃えるためには2乗した処理を元に戻す、すなわち平方根√をとればよく、それが「標準偏差」となります。
共分散: 2種類のデータの関係を表し、以下の公式で求められます。
x、yに対応するデータを散布図にプロットする際、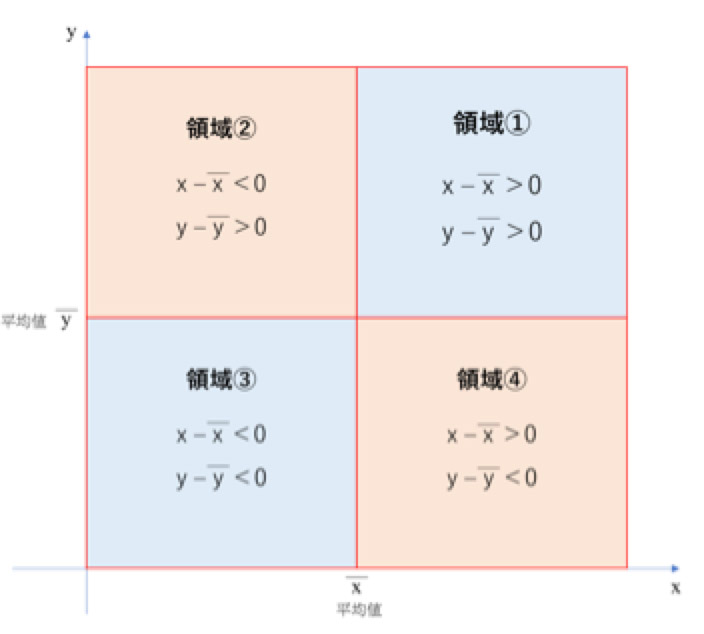
領域①と③にデータが集まっていればxとyは正の相関が強く、
領域②と④にデータが集まっていればxとyは負の相関が強いといえ、
どちらのケースも共分散の値が(正負で)大きくなります。
ただ、データの種類や単位によって共分散の値はブレが生じるため、x、yの標準偏差の積で調整した「相関係数」を用いるのが望ましいわけです。
最後の問題(4)は、解答に必要な公式や計算値が問題文中に親切に示されています。
まず、『(女子長距離グループの)身長のデータを各々2乗した値の平均値』を求めます。
設問(2)において、身長をHとして、X=(H/100)2と定義されており、設問(3)では、Xの平均値は「2.75」となっています。
従って、H2=2.75×10000=27500で、正解は「7」となります。
次に、このグループの身長の分散ですが、こちらは掲載されている公式を使えばよいですし、しかも身長の平均値(165.7)の2乗は27456.49と示されているので、
27500-27456.49=43.51で、正解は「2」となります。
いかがでしたか。
学生時代に統計が苦手だった人にとっても、意外と簡単に思われたのではないでしょうか。
【次はこちらもおすすめ】





