先日、老舗のうなぎ屋さんに行ってきました。
うな重のメニューを見ると、
並 2,500円
上 3,300円
特上 4,500円
となっており、たまには奮発しようと思っていたものの、私は結局「並」を注文しました。
日本では昔から「松・竹・梅」3段階の価格設定に馴染みがありますが、「松」「梅」よりも真ん中の「竹」を選びやすい傾向は、最近の行動経済学で「極端回避性」「フレーミング効果」などと説明されます。
私も、懐に余裕があれば「上」うな重を食べたいところでした。
さて、あなたがこのお店の経営者だとした場合、「上」うな重の売上を伸ばすためには「並(=2,500円)」と「特上(=4,500円)」の間のいくらに値段を設定したらよいと思われますか。
単純平均(相加平均)で考えると、(2,500+4,500)/2=3,500(円)になりますね。
この値段でもよさそうな気がしますが、行動経済学では、消費者心理を考えると同じ値幅で段階的に価格を上げていく直線的なプライシングはよくないとされています。
そこで、単純平均(相加平均)ではなく“相乗平均”“調和平均”を応用することを考えてみましょう。
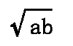
“相乗平均”は、経済成長率や物価変動率など主に変化率の平均を求める場合に使われ、aとbの相乗平均は
となります。
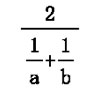
“調和平均”の考え方については、平均速度を求める学校の授業で習ったことを覚えているでしょうか。
例えば、「片道30kmの距離を、行きは時速10km、帰りは時速6kmで往復した時の平均速度」を求める場合、時速の数字だけを見て(10+6)÷2=8 (km/h)としてはいけません。
行きは30÷10=3時間、帰りは30÷6=5時間、合計8時間かけて往復60km移動したわけですから、60÷8=7.5 (km/h)が正解です。
aとbの調和平均を公式化すると
となります。
相加平均、相乗平均、調和平均の間には
相加平均 ≧ 相乗平均 ≧ 調和平均
の関係があり、「松・竹・梅」のプライシングに応用する場合、一般的な目安としては「松」と「梅」の“調和平均”から“相乗平均”の間に「竹」の値段を設定するとよさそうです。
先程のうな重の「並(=2,500円)」と「特上(=4,500円)」をa、bに当てはめると
相加平均:3,500円
相乗平均:3,354円
調和平均:3,214円
となります。
お店側が実際どのようにして「並」「上」「特上」それぞれの値決めをしたのかは分かりませんが、「上(=3,300円)」というのはなかなか巧妙な値段設定ではないかと思います。
なお、「松・竹・梅」のように段階的ではなく、単一の価格を決める場合でも、例えば「安い(安すぎる)と思う価格」「高い(高すぎる)と思う価格」の“相乗平均”“調和平均”を求めることで価格決定の際の参考にできるでしょう。
【次はこちらもおすすめ】





